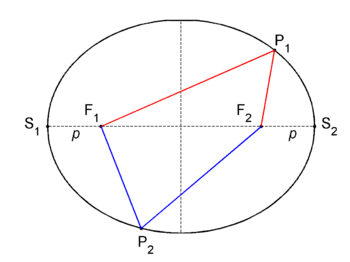
Ellipse

PD Image
Fig. 1. Ellipse. The sum of the lengths of the two red line segments (ending in P₁) is equal to the sum of the lengths of the two blue line segments (ending in P₂).

In mathematics, an ellipse is a planar locus of points that have the same sum of distances to two given points. In figure 1 two fixed points F₁ and F₂ are shown, these are the foci of the ellipse. An arbitrary point P₁ on the ellipse has distance |F₁P₁| to F₁ and distance |F₂P₁| to F₂. Let d be the sum of distances of P₁ to the foci,

$d\equiv |\mathrm {F} _{1}\mathrm {P} _{1}|+|\mathrm {F} _{2}\mathrm {P} _{1}|$

Another arbitrary point P₂ on the ellipse has distance |F₁P₂| to F₁ and distance |F₂P₂| to F₂. By definition the sum of distances of P₂ to the foci is equal d,

$|\mathrm {F} _{1}\mathrm {P} _{2}|+|\mathrm {F} _{2}\mathrm {P} _{2}|=d.\,$

The horizontal line through the foci is known as the major axis of the ellipse. Traditionally, the length of the segment of the major axis bounded by its two intersections with the ellipse is indicated by 2a. Very often the horizontal segment itself is referred to as major axis, instead of the whole line of which it is part; from here on we will follow that usage. The vertical dashed line segment, drawn halfway the foci perpendicular to the major axis, is referred to as the minor axis of the ellipse. Clearly both axes are symmetry axes, reflection in either two of them transforms the ellipse into itself.

The right hand intersection of the major axis and the ellipse is a point designated by S₂. Let the point S₁ be the corresponding left hand intersection; both points are connected by reflection in the minor axis. The distance of focus F₂ to S₂ is |S₂F₂| ≡ p. By symmetry the distance |S₁F₁| is also equal to p. The distance of S₂ to F₁ is equal to 2a − p. The distance of S₂ to F₂ is equal to p. By the definition of the ellipse the sum is equal to d, hence

$d=2a-p+p=2a.$

The sum of distances d is equal to the distance between S₁ and S₂.