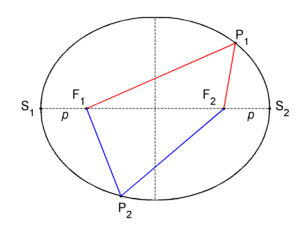
Ellipse
In mathematics, an ellipse is a planar locus of points characterized by having an equal sum of distances to two given fixed points in the plane. In figure 1 two fixed points F1 and F2 are shown, these are the foci of the ellipse. An arbitrary point P1 on the ellipse has distance |F1P1| to F1 and distance |F2P1| to F2. Let d be the sum of distances of P1 to the foci,
then all points of the ellipse have the sum of distances d. Thus, another arbitrary point P2 on the ellipse has distance |F1P2| to F1 and distance |F2P2| to F2. By definition the sum of distances of P2 to the foci is equal to d,
The horizontal line segment S1–S2 in figure 1, going through the foci, is known as the major axis of the ellipse. Traditionally, the length of the major axis is indicated by 2a. The vertical dashed line segment, drawn halfway the foci perpendicular to the major axis, is referred to as the minor axis of the ellipse; its length is usually indicated by 2b. The major and minor axes are distinguished by a ≥ b. When a = b the ellipse is a circle—a special case of an ellipse. Clearly both axes are symmetry axes, reflection in either of them transforms the ellipse into itself. Basically, this a consequence of the fact that a reflection conserves (sums of) distances.
Clearly, the two foci and the points S1 and S2 are connected by reflection in the minor axis. Hence the distance |S2F2| ≡ p is by symmetry equal to the distance |S1F1|. The distance of S2 to F1 is equal to 2a − p. The distance of S2 to F2 is equal to p. By the definition of the ellipse the sum is equal to d, hence
The sum d of distances from any point on the ellipse to the foci is equal to the length of the major axis.