Pole-in-the-barn paradox
The pole-in-the-barn paradox is a scenario presented to illustrate Albert Einstein's theory of special relativity. Like other so-called "paradoxes" of relativity, there is no actual paradox. An apparent paradox arises when (incorrectly) applying non-relativistic ideas to a relativistic situation and is resolved when relativity theory is correctly applied instead. The paradox illustrates how events that appear to happen simultaneously for one observer do not happen simultaneously for a second observer in motion relative to the first.
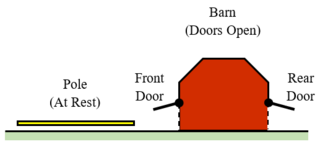
The scenario includes a long, horizontal pole and a barn with both a front and a rear door, as shown in Figure 8.1. The pole's length is Lp in its rest frame, and the distance between the barn's two doors is Lb < Lp. As such, when at rest the pole cannot fit inside the barn. When the pole is partially inside the barn and at rest, at least one of the two barn doors must be open, as one or possibly both ends of the pole will extend outside of the barn.
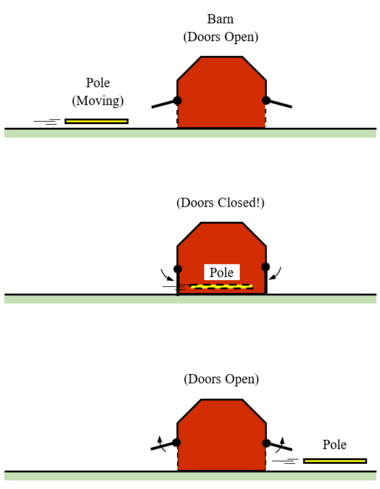
Now imagine that the pole is moving horizontally at a constant relativistic speed toward the barn, whose doors are both open as shown in the top of Figure 8.2. The pole's speed is fast enough so that, in the barn's rest frame, the pole is length-contracted to Lp' < Lb. As the pole moves through the barn, there is a brief amount of time where it is completely inside the barn as seen by an observer at rest inside the barn. When the pole is completely inside the barn, the two barn doors are both briefly shut at the same time, and then reopened before the pole starts exiting the rear of the barn.
Next, we look at things as observers moving with the pole. In this reference frame, the length of the barn is contracted to Lb' < Lb, which is still less than Lp. In other words, the pole is seen to be longer than the space inside the barn. But then how is it possible for the two barn doors to close without either hitting / getting hit by the pole?
This paradox is resolved by noting that, in the pole's rest frame, the two doors do not get shut at the same instant. Instead, the rear door is shut and reopened before the front of the pole reaches the rear door and the rear of the pole has yet to enter the barn. A short time later, when the rear of the pole is inside the barn, the front door is shut and reopened -- and by this time the front of the pole has passed outside, beyond the rear door.
The fact that the two doors are shut and reopened at the same time in the barn's frame, but at different times in the pole's rest frame, illustrates the idea that simultaneous events in one reference frame are not simultaneous in other reference frames.